SAT(R) Math Cheat Sheet

Numbers & Arithmetic

Percents

To get the percent of a value:

$S*d=F$

where $S$ is the starting amount, $d$ is the percent expressed as a decimal, and $F$ is the final result.

To calculate a percentage increase or decrease:

$S*m=F$

where $S$ is the starting amount, $m$ is the percent change expressed as a multiplier, and $F$ is the final result.

To convert a percentage change into a multiplier:

	% Change	Calculation	Multiplier
formula	$p\%$	$1+\frac{p}{100}$	$m$
increase	$12\%$	$1+\frac{12}{100}$	$1.12$
increase	$35\%$	$1+\frac{35}{100}$	$1.35$
increase	$150\%$	$1+\frac{150}{100}$	$2.5$
increase	$0.5\%$	$1+\frac{0.5}{100}$	$1.005$
decrease	$-12\%$	$1-\frac{12}{100}$	$0.88$
decrease	$-40\%$	$1-\frac{40}{100}$	$0.60$

To convert a multiplier into a percentage change:

	Multiplier	Calculation	% Change
formula	$m$	$(m-1)*100$	$p\%$
increase	$1.12$	$(1.12-1)*100$	$+12\%$
increase	$1.35$	$(1.35-1)*100$	$+35\%$
increase	$2.5$	$(2.5-1)*100$	$+150\%$
increase	$1.005$	$(1.005-1)*100$	$+0.5\%$
decrease	$0.88$	$(0.88-1)*100$	$-12\%$
decrease	$0.6$	$(0.6-1)*100$	$-40\%$

Fractions

Cross multiplication:

$$\frac{a}{b} = \frac{c}{d}$$ $$a*d=c*a$$

Dividing by a fraction:

$$\frac{\frac{a}{b}}{\frac{c}{d}}= \frac{a}{b}*\frac{d}{c}$$

Linear Functions

Slope formula

Given two points, $(x_1, y_1)$ and $(x_2, y_2)$, the slope of a linear equation is:

$$m=\frac{y_2-y_1}{x_2-x_1}$$

Slope-intercept Form

Given an equation in the form $y=mx+c$:

• the slope of the line is $m$
• the slope of the perpendicular line is $-1/m$
• the $y$-intercept is $c$
• the $x$-intercept is $-c/m$

Standard Form

Given an equation in the form $ax+by=k$:

• the $y$-intercept is $k/b$
• the $x$-intercept is $k/a$
• the slope of the line is $-a/b$
• the slope of the perpendicular line is $b/a$

Quadratic Functions

General Form

Given a quadratic function in the form $f(x)=ax^2+bx+c$:

• the axis of symmetry is at $x=-b/2a$
• the vertex is at $(-b/2a, f(-b/2a))$
• the sum of the solutions is $-b/a$
• the product of the solutions is $c/a$
• the solutions, if they exist, are

$$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$$

• To determine how many solutions a quadratic has:

$\sqrt{b^{2}-4ac} > 0$ => Two solutions

$\sqrt{b^{2}-4ac} = 0$ => One solution

$\sqrt{b^{2}-4ac} < 0$ => No solutions

• To determine the distance between the solutions:

$$\frac{\sqrt{b^{2}-4ac}}{a}$$

$x$-intercept Form

Given a quadratic function in the form $f(x)=a(x-p)(x-q)$:

• the solutions are $x=\{p, q\}$
• the axis of symmetry is $\frac{p+q}{2}$
• the coordinates of the vertex are $(\frac{p+q}{2}, f(\frac{p+q}{2}))$
• the product of solutions is $pq$
• the sum of solutions is $p+q$

Vertex Form

Given a quadratic function in the form $f(x)=a(x-h)^2+k$:

• the coordinates of the vertex are $(h, k)$
• the axis of symmetry is $h$
• the solutions, if they exist, are $x=h\pm\sqrt{-\frac{k}{a}}\$
• if $k=0$, the quadratic has 1 solution
• if $-k/a > 0$, then the quadratic has two solutions
• if $-k/a < 0$, then the quadratic has no solutions
• the product of solutions is $h^{2}+\frac{k}{a}$
• the sum of solutions is $2h$
• the distance between the solutions is $2\sqrt{-\frac{k}{a}}$

Exponential Functions

Given an exponential function in the form $f\left(x\right)=ab^{kx}+d$:

• the $y$-intercept is $a+d$
• the growth rate is $b$, expressed as a multiplier
  • if $0 < b < 1$, then the function is decreasing.
  • if $b > 1$, then the function is increasing.
• $k$ is how many times the function $f$ increases or decreases per step in the $x$.

Stats & Probability

Mean

• the mean is the simple or weighted average of a set of numbers:

$$\bar{x} = \frac{\sum{xf}}{\sum{f}}$$

Where $x$ is the value of each item and $f$ is the amount of times the item appears (the frequency).

For example, if $A = \{1, 2, 2, 2, 3, 5, 5, 7\}$, then the mean is:

$$\bar{x}=\frac{1*1+3*2+1*3+2*5+1*7}{8}$$

Mode

Given a set of numbers, the mode is the number that appears most frequently:

For example, if $A = \{1, 2, 2, 2, 3, 5, 5, 7\}$, then the mode of set $A$ is $2$.

Median

Given a set of ordered numbers, the median is the middle number:

For example, if $A = \{1, 2, 2, 2, 3, 5, 5, 7\}$, then the median of set $A$ is $2.5$.

Standard Deviation

Given a set of numbers, the standard deviation tells us how spread out the data are. For example, for these two data sets:

$A = \{10, 12, 12, 12, 13, 15, 15, 17\}$

$B = \{1, 5, 7, 12, 13, 18, 22, 27\}$

Both are more or less centered around $12$ but set $B$ has a larger standard deviation because the numbers are more spread out.

You shouldn't ever need to calculate the standard deviation, but you should be able to tell whether one data set has a higher standard deviation than the other.

Geometry & Trigonometry

SOHCAHTOA

SOHCAHTOA is pretty much all you need on the SAT for trig problems.

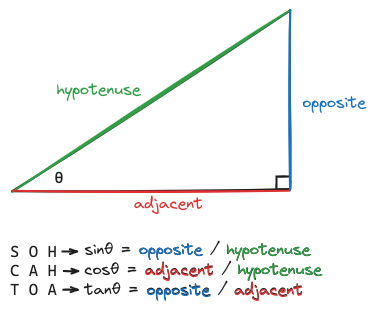
From these relationships, we can also determine that:

$$sin(x)=cos(90-x)$$

which is equivalent to:

$$x+y=90 sin(x)=cos(y)$$

30-60-90 Triangle

Any triangle whose angles are 30°, 60°, and 90° will have side lengths in the following ratios:

	shortest side	middle side	hypotenuse
general case	$x$	$x\sqrt{3}$	$2x$
example 1	$2$	$2\sqrt{3}$	$4$
example 2	$\frac{7\sqrt{3}}{3}$	$7$	$\frac{14\sqrt{3}}{3}$

45-45-90 Triangle

Any triangle whose angles are 45°, 45°, and 90° will have side lengths in the following ratios:

	shortest side	hypotenuse
general case	$x$	$x\sqrt{2}$
example 1	$5$	$5\sqrt{2}$
example 2	$\frac{7\sqrt{2}}{2}$	$7$

Pythagorean Triples

Any triangle whose side lengths are in the following ratios will be right angled triangles:

side A	side B	side C	note
3	4	5	super common
5	12	13	uncommon
8	15	17	super rare

Circle Arcs and Sectors

Given a slice of a circle, like so:

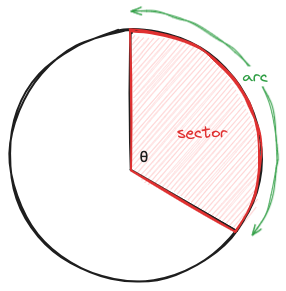
We can say that:

$$\frac{arc}{2\pi{r}} = \frac{sector}{\pi{r^2}} = \frac{\theta°}{360°} = \frac{\theta{\ rads}}{2\pi}$$